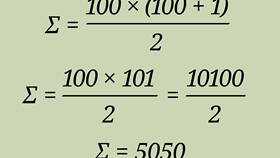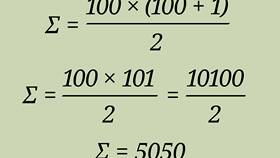В математических задачах часто встречаются формулировки вида "Известно что... Найдите сумму". Рассмотрим типовые подходы к решению таких задач.
Содержание
В математических задачах часто встречаются формулировки вида "Известно что... Найдите сумму". Рассмотрим типовые подходы к решению таких задач.
Общий алгоритм решения
- Внимательно проанализировать условие задачи
- Выявить все данные и зависимости между ними
- Составить уравнения или систему уравнений
- Решить полученные уравнения
- Найти требуемую сумму
- Проверить правильность решения
Примеры типовых задач
Пример 1: Арифметическая прогрессия
Известно, что a₁ = 5, d = 3. Найдите сумму первых 8 членов прогрессии.
| Решение: | Используем формулу суммы арифметической прогрессии: Sₙ = (2a₁ + d(n-1))·n/2 S₈ = (2·5 + 3·7)·8/2 = (10 + 21)·4 = 31·4 = 124 |
Пример 2: Геометрическая прогрессия
Известно, что b₃ = 12, b₅ = 48. Найдите сумму первых 6 членов.
| Решение: | 1. Найдем знаменатель: b₅ = b₃·q² ⇒ 48 = 12·q² ⇒ q = ±2 2. Найдем b₁: b₃ = b₁·q² ⇒ 12 = b₁·4 ⇒ b₁ = 3 3. Сумма S₆ = b₁(q⁶-1)/(q-1) = 3(64-1)/1 = 189 (для q=2) |
Основные формулы для нахождения сумм
| Тип последовательности | Формула суммы |
| Арифметическая прогрессия | Sₙ = (a₁ + aₙ)·n/2 |
| Геометрическая прогрессия | Sₙ = b₁(1-qⁿ)/(1-q) при q≠1 |
| Натуральный ряд | 1+2+...+n = n(n+1)/2 |
| Квадраты натуральных чисел | 1²+2²+...+n² = n(n+1)(2n+1)/6 |
Практические рекомендации
- Внимательно определяйте тип последовательности
- Проверяйте достаточность данных для решения
- Рассматривайте все возможные варианты (например, ±q в геом. прогрессии)
- Используйте подстановку для проверки правильности решения
- При работе с системами уравнений выбирайте наиболее рациональный метод решения
Частые ошибки
| Ошибка | Как избежать |
| Неправильное определение типа прогрессии | Анализировать соотношение между членами |
| Ошибки в знаках | Внимательно работать с отрицательными числами |
| Неправильное применение формул | Запоминать точные формулировки формул |
| Арифметические просчеты | Проверять вычисления |
Решение задач на нахождение суммы по известным данным требует понимания свойств последовательностей и внимательной работы с формулами. Регулярная практика помогает выработать навык быстрого и точного решения таких задач.
